솔의눈 님의 블로그

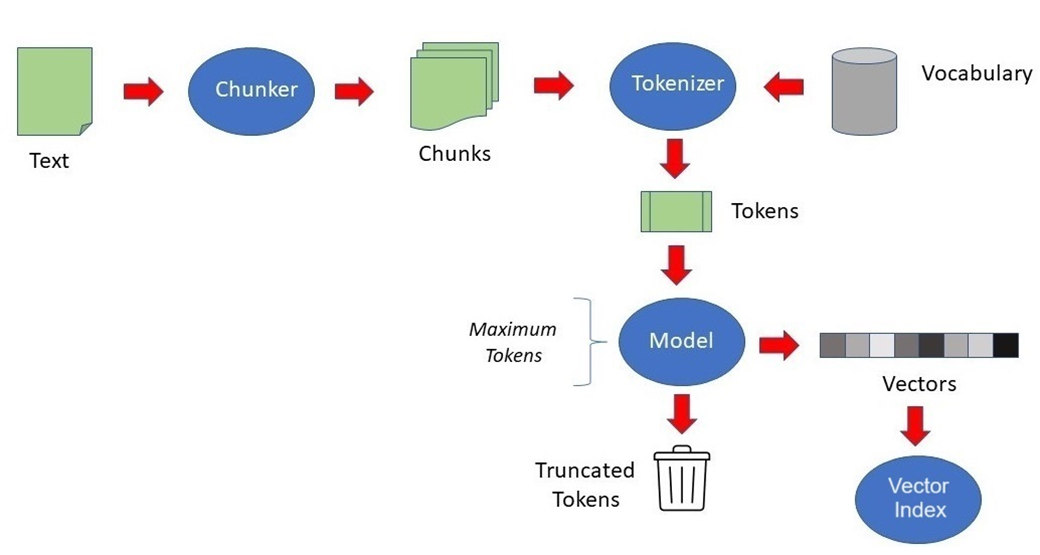
벡터인덱스 개념

벡터 임베딩에 대한 벡터 인덱스를 생성하고 이 인덱스를 사용하여 방대한 벡터 공간에서 유사성 검색을 실행할 수 있습니다.

벡터 인덱스는 고차원 벡터를 사용하여 유사성 검색을 가속화하도록 설계된 특수 인덱싱 데이터 구조의 한 종류입니다. 클러스터링, 분할 및 이웃 그래프와 같은 기술을 사용하여 유사한 항목을 나타내는 벡터를 그룹화하여 검색 공간을 크게 줄여 검색 프로세스를 매우 효율적으로 만듭니다.

 현재 오라클에서 지원하는 벡터 인덱스의 종류는 2가지 입니다.
1.      In-Memory Neighbor Graph = Hierarchical Navigable Small World (HNSW)
2.      Neighbor Partition vector index = Inverted File Flat (IVF) index

 IN-Memory Neighbor Graph Index는 계층적 탐색 가능한 소규모 세계(HNSW)유형을 지원하는 인덱스로 벡터 근사 유사성 검색을 위한 매우 효율적인 인덱스입니다.
HNSW 그래프는 계층적(Hierarchical) 구조와 함께 탐색 가능한 소규모 세계(NSW) 네트워크의 원칙을 사용하여 구조화됩니다.

 Neighbor Partition vector index는 Inverted File Flat(IVF) Index 를 유일하게 지원하는 벡터 유형의 인덱스입니다. IVF는 높은 검색 품질과 적당한 속도의 균형을 이루는 분할 기반 인덱스입니다.
이웃 파티션 또는 클러스터를 사용하여 검색 영역을 좁혀 검색 효율성을 높이기 위해 고안된 기술입니다.

HNSW (Hierachical Navigable Small World) 인덱스 이해

HNSW는 Hierarchical Navigable Small World의 약자로 여러 알고리즘들의 결합으로 만들어져 있습니다.
결합된 알고리즘을 분해해서 살펴보면 Small World 특성을 바탕으로 효율적인 경로를 탐색 가능하게 하는  NSW(Navigable Small World)라는 알고리즘에 Skip List의 개념을 적용하여 NSW 그래프를 계층화한 HNSW (Hierachical Navigable Small World) 알고리즘이 만들어지게 되었습니다.

 Navigable Small World(NSW)를 사용하면 그래프의 각 벡터가 세 가지 특성을 기반으로 여러 다른 벡터에 연결되는 근접 그래프를 구축하는 것이 목표입니다.
1.     벡터 사이의 거리
2.     삽입 중 검색 과정에서 각 단계에서 고려되는 가장 가까운 벡터 후보들의 최대 수 (EFCONSTRUCTION)
3.     벡터당 허용되는 최대 연결 수(NEIGHBORS)

위의 두 임계값의 조합이 너무 높으면 밀집 연결 그래프가 되어 검색 프로세스가 느려질 수 있습니다.

반면, 해당 임계값의 조합이 너무 낮으면 그래프가 너무 희소하거나 연결이 끊어져서 검색 중에 특정 벡터 간의 경로를 찾기 어려울 수 있습니다.

HNSW 벡터 인덱스는 In-Memory 인덱스이므로 인덱스 세그먼트가 생성되지 않으며, 암시적으로 추가 오브젝트를 생성합니다. *_INDEXES 뷰를 조회하면 2개의 B-tree 인덱스와 3개의 테이블이 생성된 것을 확인할 수 있습니다.

Small World 6단계의 법칙

출처 §   THE ORACLE OF BACON(https://oracleofbacon.org/) §   NHN Forward 22 - 벡터 검색 엔진에 ANN HNSW 알고리즘 도입기(https://inspirit941.tistory.com/504) §   자료구조와 알고리즘 - 벡터 검색 엔진 최적화 방법: HNSW(Hierarchical Navigable Small World Graphs) (https://kokoko12334.tistory.com/m/entry/hsfl) §   Hierarchical Navigable Small World Graph로 nearest neighbor를 빠르게 찾아 보자. (https://ita9naiwa.github.io/ml/2019/10/04/hnsw.html) §   검색증강생성(RAG) - 그래프 기반 벡터 인덱스 HNSW(Hierarchical Navigable Small World) (https://jerry-ai.com/30)

스몰월드는 케빈 베이컨 게임으로 설명으로 쉽게 설명이 됩니다.

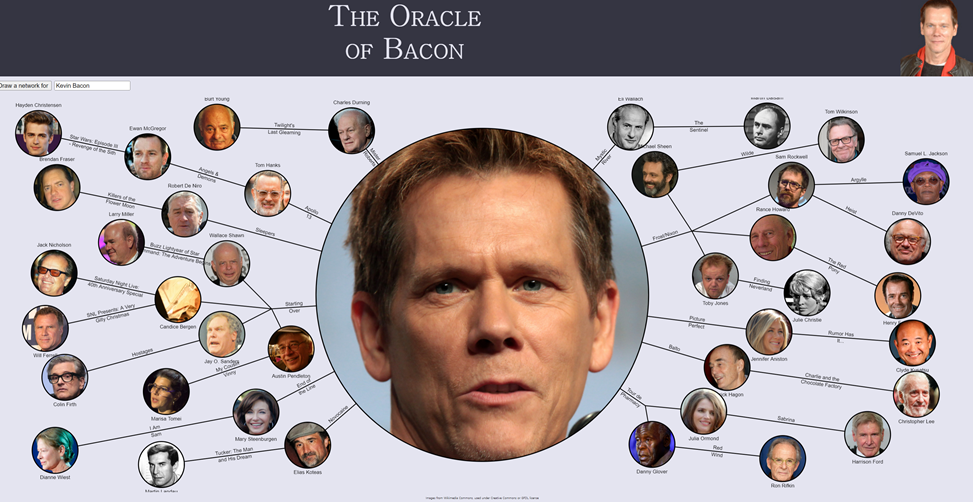
우리나라의 유명 배우 중 한명인 송강호 배우가 있습니다. 송강호 배우는 케빈 베이컨과 몇 단계를 거치면 도달할 수 있을까요? 놀랍게도 3단계만에 송강호 배우와 케빈 베이컨배우가 연결이 됩니다.

케빈 베이컨은 어퓨굿맨 이라는 영화에서 톰 크루즈와 함께 출연을 했습니다. 톰 크루즈는 바닐라 스카이라는 영화에서 틸다 스윈튼배우와 같이 출연을 했습니다. 틸다 스윈튼배우는 설국열차에서 송강호 배우와 같이 출연을 했습니다. 정리를 해보면 아래와 같은 관계가 형성이 됩니다.

케빈 베이컨-어퓨굿맨-톰 크루즈-바닐라스카이-틸다 스윈튼-설국열차-송강호

그렇다면 케빈 베이컨과 우리나라 배우들과의 관계도 많아야 4~5단계안에 형성이 될 수 있습니다.
이 관계를 일반화해서 전세계에 있는 사람들을 대상으로 생각해 보겠습니다. 전세계에 있는 사람들도 평균적으로 6단계를 거치면 만날 수 있다라는 네트워크 이론 “6단계 법칙”이 만들어지게 되었습니다.

 

위의 베이컨 게임을 통해서 보았듯 우리는 수학적으로 6단계안에 관계가 형성되고 있고, 이러한 법칙을 바탕으로 Small World(작은 세계)라는 개념이 탄생하게 되었습니다. 스몰월드라는 네트워크 이론을 조금 더 살펴보겠습니다.

아래의 그래프처럼 모든 네트웍은 그 연결 방식에 따라 크게 세 가지로 나눠질 수 있습니다.
일정한 규칙에 따라 인접한 곳과 일정한 숫자로만 링크되는 'regular network'이 있고,
무작위로 서로 연결되어 있는 'random network'이 있습니다.
그리고 이 둘의 중간쯤에 있는 Small-world가 있습니다.
스몰월드는 구성원의 일부만이 전혀 엉뚱한 곳으로 연결되어 있는 네트워크입니다.

Small World Network를 도식화 한 그래프에서 스몰월드의 상태를 알아보겠습니다.
가장 왼쪽에 있는 그래프는 모든 Edge(간선,선)이 고르게(Regular) 연결되어 있는 상태입니다.
가장 오른쪽 그래프는 모든 Edge가 Random으로 연결된 상태입니다.

왼쪽에 있는 Regular 그래프에서 몇개의 노드를 Random 연결시켜 봤더니 평균적으로 노드에 도달하는 거리의 수가 확연히 줄어드는것을 볼 수 있습니다.

중간에 있는 Small-world 그래프는 위에 설명처럼 Regular그래프에서 3개의 노드를 랜덤으로 추가하여 연결했더니 전체적인 노드의 길이가 줄어들었습니다.

즉, 전체 네트워크가 거대하더라도 일부의 특정 노드에 의해서 전체가 서로 가깝게 연결될 수 있다는 것을 의미합니다.

Small world의 이론적인 특징을 정리해보면 다음과 같습니다.
1.      짧은 평균 경로 길이 : 베이컨 게임에서 보았듯 Small world 네트워크에서 네트워크 내의 임의의 두 노드 사이의 평균거리는 매우 짧습니다.
2.      높은 클러스터링(높은 군집계수) : 이 네트워크는 노드들이 지역적으로 밀집된 클러스터를 형성하는 경향이 있습니다. 즉, 한 노드의 이웃 노드들이 서로 연결되어 있을 가능성이 큽니다. “내 친구의 친구도 내 친구일 가능성이 높다”라는 상황으로 나타날 수 있습니다.
3.      긴 거리 연결 : 비교적 멀리 떨어져있는 노드들이 특별한 연결을 통해 서로 직접 연결되는 것을 의미합니다. 긴 거리 연결(long-range link)" 또는 "지름길(shortcut)로 불리는 이 연결을 통해 전체의 연결성을 크게 개선됩니다.

NSW는 Small-World Network 특성을 유지하면서 현재 위치에서 가장 가까운 이웃 노드로 이동하여 최단 경로를 찾을 수 있는 네트워크 구조를 말합니다.

아래의 그림은 각 벡터값을 표현한 그림입니다.

검정색 선은 Regular로 표현된 경로이고, 빨간색 선은 Small World의 특징 중 하나인 Long-range link를 표현한 것 입니다. 시작점인 entry point에서 목표점인 query 벡터를 찾아가보도록 하겠습니다.

검은색 노드들만 따라갔을 때 4개의 노드를 거쳐서야 가장 가까운 이웃 노드로 이동이 되었는 반면,small world를 적용한 빨간색 노드와 섞어서 찾아 갔을때 3개의 노드만 거쳐서 가장 가까운 이웃 노드로 이동이 된 것을 확인할 수 있습니다.

하지만 NSW 알고리즘에도 단점이 있습니다.

바로 local minimum에 빠질 수 있다는 문제입니다.

NSW의 문제점인 local minimum에 대해 알아보겠습니다.

 Local Minimum : 미니멈은 탐색 과정이 더 이상 진전되지 않는 지점을 의미.
네트워크 탐색 과정에서 발생할 수 있는 문제 중 하나로, 목적지에 도달하기 위해 최단 경로를 찾으려는 탐색이 더 이상 진행되지 않고 멈추는 지점을 의미합니다. 이 지점에서는 더 이상 목적지로 가까워지지 않거나, 오히려 목적지에서 멀어지게 되는 상황이 발생할 수 있습니다.
실생활을 통해서 예를 들면, 회사의 위치가 서울시 서초구에 위치해 있는데 주소에 대한 링크수가 작다고 하면  회사의 주소는 서울시다 라는 Local minimum에 빠질 위험성이 있습니다. 반대로 링크 수를 많이 늘리면 서초구 서초**빌딩 이라는 주소가 나오겠지만 찾아가는 단계는 서울시를 찾는 단계보다 복잡해집니다.

서버의 입장에서 보면 링크수가 늘어나면 정확도는 높아지지만 탐색 시간과 자원은 늘어나게 되는것입니다. 그렇기에 정확도와 자원의 적정선을 찾는 튜닝이 필요합니다.

아래에 그래프를 통해 Local Minimum이 발생하는 것을 확인해보겠습니다.

쿼리 벡터 V와 네트워크 내 가장 가까운 노드를 탐색할 때, 해당 Entry 진입점에서 시작하여 Greedy 탐색을 통해 가장 가까운 노드를 찾을 수 있습니다.

하지만 위의 진입점에서 출발하여 Greedy 방식을 적용하면 가장 가까운 노드가 아닌 노드를 선택합니다.
이를 Local minimum 이라고 합니다. 이를 해결하는 방법 중에 하나는 연결하는 링크 수(m)를 늘리는 것입니다. 하지만 이는 정확도가 높아지지만 그만큼 탐색 시간이 늘어나게 됩니다.

이 문제를 해결하기 위해서 계층 구조(Hierachical)를 추가합니다.

계층 구조를 알아보기 전 Greedy알고리즘을 보고 넘어가겠습니다.

Greedy 알고리즘

Greedy 알고리즘 : 최적의 값을 구해야 하는 상황에서 사용되는 근시안적인 방법론.
아래의 그림으로 Greedy 알고리즘을 사용해서 “노드에서 합이 가장 높은 방법”을 찾는 문제를 해결해보겠습니다.

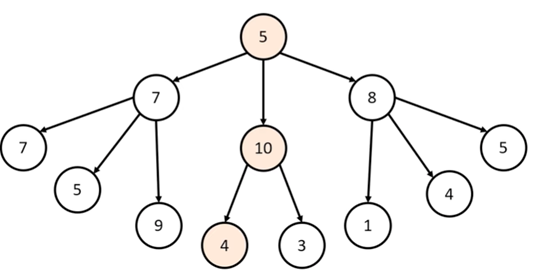
1.      처음에는 루트노드에서 시작하므로 5인 정점을 선택이 됩니다.
2.      두번째는 브런치노드에서 3개의 정점 7,10,8에 대해 비교 후 현재 노드에서 가장 큰 10을 선택합니다.
3.      마지막으로 리프노드에서 2개의 정점 4,3에 대해 비교 후 4를 선택합니다.

Greedy(탐욕) 알고리즘은 현재 상황에서 가장 적합한 답안을 찾으므로 정답과는 다를 수 있습니다. 아래의 그림에서는 5->7->9의 합인 21이 정답이지만 greedy 알고리즘을 사용했을 시에는 노드당 가장 큰 값을 선택하므로 5->10->4로 합이 19인 답안이 나오게 됩니다.

앞에서 NSW의 문제점인 Local minimum을 해결하기 위해 계층을 추가하여 HNSW (Hierarchical Navigable Small World)를 만들었습니다.
HNSW(Hierachical Navigable Small World)는 근사 최근접 이웃 탐색(Approximate Nearest Neighbor Search)을 위해 사용되는 알고리즘으로 NSW에 문제점인 로컬미니멈을 해결하기 위해 skip list의 개념을 적용하여, NSW 그래프를 계층화한 알고리즘입니다.
계층을 효율적으로 나누기 위해서 Skip list 개념을 사용하는데 잠깐 알아보고 HNSW로 넘어가겠습니다.

기존의 단일 연결 리스트에서 숫자 6에 접근하려면, 진입점부터 시작해 각 노드를 순차적으로 접근해야 합니다.
스킵 리스트는 이러한 단점을 해결하기 위해 다중 레벨을 도입하여 더 빠르게 탐색할 수 있게 합니다. 스킵 리스트는 여러 레벨의 연결 리스트로 구성되어 있으며, 각 레벨은 하위 레벨의 노드를 건너뛸 수 있는 포인터를 포함합니다. 

Skip list 에는 두가지에 유형이 있습니다.

하나는 완전 스킵리스트이고, 나머지 하나는 랜덤 스킵리스트(=확률 스킵리스트) 입니다.

HNSW에서 사용하는 스킵리스트의 유형은 확률 스킵리스트이므로, 완전 스킵리스트는 간략하게만 살펴보겠습니다.

• 완전 스킵리스트 : 스킵하는 레벨을 규칙적으로 정해서 구성하는 방법입니다.

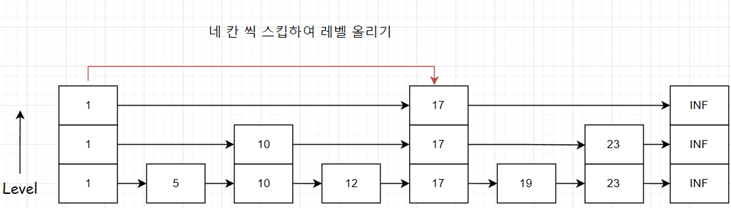
완전 스킵리스트의 방식은 고정된 패턴으로 인해 유연성이 부족하고 특정 상황에서는 비효율적일 수 있습니다.
검색은 빠르지만, 삽입과 삭제 연산에서 비효율적인 구조를 갖게 됩니다. 삽입과 삭제 하는 연산에서 스킵 리스트를 재구성해야하기 때문입니다.

이를 해결하기 위한 방법이 랜덤 스킵리스트입니다. 

• 확률(랜덤) 스킵리스트 : 각 레벨의 노드가 확률적으로 결정되는 방식.

랜덤 스킵리스트는 확률적 접근 방법을 통해 삽입 및 삭제 과정을 더욱 효율적으로 만들어줍니다.
아래에 그래프를 통해 확인해보겠습니다.

- 레벨 1에서는 모든 노드가 존재하므로 확률이 1입니다.
- 레벨 2에서 노드를 가질 확률은 1/2입니다.
- 레벨 3에서 노드를 가질 확률은 1/4입니다.
- 레벨 k에서 노드를 가질 확률은 1/(2^(k-1))입니다.

예를 들어, 2 레벨에 노드를 배치할 확률이 1/2, 3 레벨에서는 1/4인 식으로 재귀적으로 적용됩니다. 이를 통해 삽입 및 삭제 과정에서도 평균적인 시간 복잡도를 유지할 수 있습니다.

이와 같은 확률 할당 방식은 노드가 상위 레벨로 갈수록 점점 더 적어지도록 만들며, 이를 통해 노드들의 탐색시간을 줄일 수 있습니다.

여러 복잡한 알고리즘들을 알아본 끝에 앞에 알고리즘들의 결합인 HNSW에 대해 알아보겠습니다. 위에서 설명한 바와 같이 HNSW(Hierachical Navigable Small World)는 근사 최근접 이웃 탐색(Approximate Nearest Neighbor Search)을 위해 사용되는 알고리즘으로 NSW에 문제점인 로컬미니멈을 해결하기 위해 skip list의 개념을 적용하여, NSW 그래프를 계층화한 알고리즘입니다.

위에서 학습한 Skip list를 계층화 하여 NSW에 적용을 하면 다음과 같습니다.

시작점은 Entry Pioint인데 가장 높은 계층인 Entry Layer에서 시작을 합니다.

해당 계층에서 가장 가까운 정점을 찾고 다음 계층으로 내려갑니다.

다음계층으로 내려간 뒤 해당 계층에서 가장 가까운 정점을 찾고 다음 계층으로 내려간 후 가장 낮은 계층에서 사용자의 질의 벡터(vq)와 가장 근접한(Nearest Neighbor) 벡터를 찾습니다.

이때 계층과 노드가 작으면 Local minimum에 빠질 수 있고, 너무 많으면 시간과 자원의 소모가 커질 위험이 있습니다.

높은 레이어에서는 노드의 수가 작고, 인접한 노드 사이의 거리가 깁니다.
낮은 레이어로 갈수록 노드의 수가 많고, 인접한 노드 사이의 길이가 짧아집니다.

실생활에서 예를 들어보겠습니다.

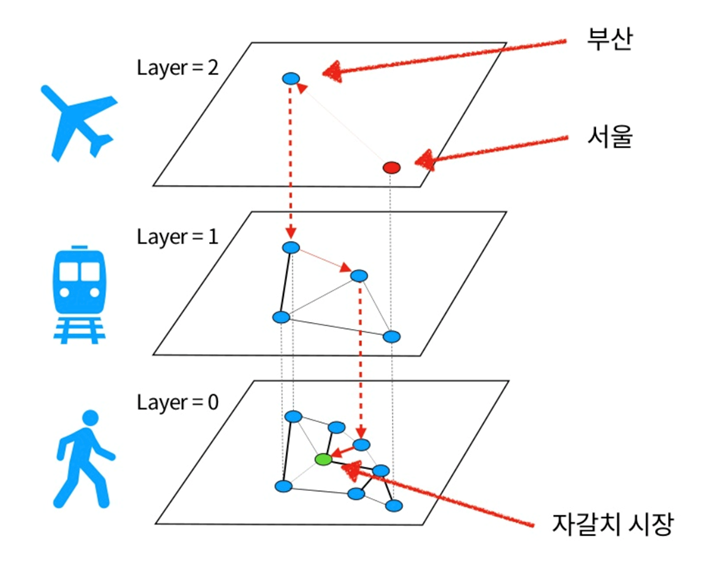
노드 사이의 거리를 효율적으로 계산하기 위해 확률 스킵리스트를 적용해서 노드들을 계층화 합니다.

강릉에서 자갈치 시장을 찾아가는 방법을 생각해봅니다. 시간이라는 자원을 아끼기 위해 가장 상위 계층에서 시작합니다. 서울을 경유해서 가는 거리로만 보면 자갈치 시장으로 바로 가는 직선거리가 가장 짧습니다. 하지만 바로 가기에는 시간이라는 자원이 많이 소모가 됩니다.

그래서 비행기를 타고 한번에 부산까지 이동을합니다. 여기서 비행기는 탈수있는 곳이 적고 한번에 멀리 이동할 수 있는 특징이 있습니다.
HNSW 그래프에서도 동일합니다. 최 상위계층의 특징은 노드간의 거리가 멀고 정점의 수가 적습니다.
부산 까지 이동을 한 후 자갈치 시장으로 가기위해서 지하철을 타고 이동을 합니다.
자갈치 시장에 가장 가까운 지하철역 내립니다.

이 과정을 HNSW에서 보면 가장 근접한(Nearest Neighbor) 벡터를 찾는 방법과 동일합니다.

마무리

ORACLE Vector Index를 공부하면서 여러 알고리즘들을 접하였는데, 이해가 쉽지않았습니다. 이곳저곳을 찾아가며 정보를 얻은것들을 바탕으로 작성했는데, 오라클에서 추구하는 HNSW와 조금 차이가 있을 수 있습니다.
ORACLE Document에서는 간략하게만 설명이 나와있어서 추가적인 정보를 붙여서 정리했는데 도움이 되었으면 좋겠습니다.

들어가며

앞선 글에서 RAG에 대해 DBA의 관점으로 간략하게 설명을 했습니다.
(RAG(검색 증강 생성)이란 글 참고)
ORACLE DB에서 RAG를 사용하는 방법에 대해 알아보겠습니다.
제가 테스트 한 버전은 23AI Free 버전이므로 추후 EE버전에서는 내용이 달라질 수 있습니다.

실습 시나리오

오라클에서 LOCAL LLM 인 OLLAMA를 사용하여 EXAONE MODEL에 RAG(증강검색)을 하는 테스트입니다.
대법원선고중요판결요지 라는 문서에 내용을 Chunk후 Embbeding 시켜 Vector 값을 가진 테이블을 만들었습니다. 그 테이블의 데이터를 사용해서 EXAONE LLM Model에 질의를 하는 내용으로 테스트 내용을 작성했습니다.

대법원선고중요판결요지파일은 아래의 url 링크를 통해 다운받아서 사용하세요.
파일명 : law240830(8.29.판결).pdf 다운로드 링크

실습

1. 실습 테이블 생성

위에 선고중요판결요지라는 파일을 서버에서 불러와 임베딩하여 Vector값으로 컬럼이 포함된 테이블로 생성합니다.
쿼리 가장 아래에 있는 embed_vector clob 이라는 쿼리 내용중 clob 타입을 vector로 했을 시에 테이블에 데이터가 보이지 않는 문제가 발생하여 clob 후 select 절에서 to_vector함수를 사용하여 다시 벡터화 시켰습니다.

create table dre.rag_test as
select embed_id,embed_data,to_vector(embed_vector) as embed_vector
  FROM (select 
dbms_vector_chain.utl_to_text(TO_BLOB(bfilename('DOC_DIR',a.file_name))) AS DOC_content_blob
from (values('대법원선고중요판결요지_240829.pdf')) a (file_name) ) dc 
CROSS JOIN TABLE (
                 dbms_vector_chain.utl_to_embeddings(
                 dbms_vector_chain.utl_to_chunks(
                 dbms_vector_chain.utl_to_text(dc.DOC_CONTENT_BLOB)
                    ,json('{"by":"characters","max":"250","split":"none","normalize":"all","LANGUAGE":"KOREAN"}')),
                        json('{"provider":"database", "model":"ONN.DISTILUSE_BASE_MULTILINGUAL_CASED_V2"}'))) t
CROSS JOIN JSON_TABLE(t.column_value, '$[*]' COLUMNS (embed_id NUMBER PATH '$.embed_id', embed_data VARCHAR2(1000) PATH '$.embed_data', embed_vector clob PATH '$.embed_vector')) AS et;

2. HOST_ACL 등록

LOCAL LLM 서버와의 통신을 위해 HOST_ACL을 등록합니다.

BEGIN
    dbms_network_acl_admin.append_host_ace(
        host =>'172.17.12.116',
        LOWER_PORT =>'9301',
        UPPER_PORT =>'9301',
        ace => xs$ace_type(
           privilege_list => xs$name_list('http', 'http_proxy'),
           principal_name => 'DRE',
           principal_type => xs_acl.ptype_db)
    );
END;
/

3. ACL 등록 후 통신 Test

SELECT * FROM  DBA_HOST_ACES ACES;
select utl_http.request('http://172.17.12.116:9301') from dual;

#쿼리 결과
Ollama is running

4. CREDENTIAL 생성

LLM API key 관리를 위해 CREDENTIAL 오브젝트 생성합니다.

declare
	  v_params json_object_t;
	  v_name varchar2(1000) :=  'EXAONE_CRED';
	  v_api_token varchar2(1000) := 'ollama-key'; 
	begin
	   v_params := json_object_t();
	   v_params.put('access_token',v_api_token); 
	   begin
	        DBMS_VECTOR_CHAIN.DROP_CREDENTIAL ( CREDENTIAL_NAME  => v_name);
	   exception 
	     when others then
	        null;
	   end;
	   
	   DBMS_VECTOR_CHAIN.CREATE_CREDENTIAL ( CREDENTIAL_NAME => v_name, PARAMS => json(v_params.to_string));
	end;
/

5. LLM 테스트

ORACLE에서 LLM 서버에 질의를 해 연결상태를 점검합니다. LLM모델은 exaone3.0:8b 입니다.

declare
  input clob;
  params clob;
  output clob;
begin
  utl_http.set_body_charset('UTF-8'); 
  input := '안녕 exaone3.0:8b 모델에 대해 설명해줘';
  params := '
{
  "provider": "OpenAI",
  "credential_name": "EXAONE_CRED",
  "url": "http://172.17.12.116:9301/v1/chat/completions",
  "model": "exaone3.0:8b",
  "context_length" : 2048
}';
  output := dbms_vector_chain.utl_to_generate_text(input, json(params));
  dbms_output.put_line(output);
  if output is not null then
    dbms_lob.freetemporary(output);
  end if;
exception
  when OTHERS THEN
    
    DBMS_OUTPUT.PUT_LINE (SQLERRM);
    DBMS_OUTPUT.PUT_LINE (SQLCODE);
end;
/

#질의 결과
-------------------------[Start Time: 2024/09/19 15:24:39]-------------------------
SQL> 안녕하세요! LG AI 연구원에서 개발한 EXO(EXpert Operating System) 3.0 기반의 8B 모델, EXAONE 3.0에 대해 설명해드릴게요.

### 주요 특징 및 장점:
1. **고성능 언어 이해 능력**:
   - 한국어와 영어를 포함해 다양한 자연어 처리 작업에서 우수한 성능을 자랑합니다.
  
2. **초거대 AI 모델 기반**: 
   - 8x Nvidia A100 GPU로 학습되었으며, 약 6TFLOPS의 연산 능력을 가집니다. 이는 기존 초거대 인공지능 대비 효율적이고 강력한 계산력입니다.
    
3. **전문 지식 통합**:
   - 방대한 양의 전문 문서 데이터를 바탕으로 다양한 산업의 최신 정보와 전문 지식을 습득할 수 있습니다. 
  
4. **생성적 AI 능력**:
   - 창작 활동 (예: 소설 작성, 음악 작곡 등)에도 뛰어난 성능을 보입니다. 이는 모델이 단순히 데이터를 분석하는데 그치지 않고 새로운 지식과 콘텐츠를 생성해 낼 수 있음을 의미합니다.
    
5. **한국어 특화 학습 모델**: 
   - 한국어에 최적화된 언어 모델로 감정 분석, 번역 작업 등에서도 우수한 성과를 보이며, 멀티모달 데이터 처리 기능이 강화되어 이미지 인식까지 확장할 수 있습니다.
  
6. **데이터 학습 윤리 및 프라이버시 준수**: 
    - 개인정보 보호 규정과 윤리적인 AI 개발 가이드라인을 철저히 준수하여 안전하게 활용 가능합니다.
   
### 결론적으로,
EXAONE 3.0은 여러 산업의 전문 작업 지원, 창의성 발휘 등 다양한 방면에서 효과적으로 사용될 수 있는 차세대 인공지능 모델입니다. 여러분께서 필요로 하시는 특정 분야나 적용 사례가 있다면 더 구체적인 설명도 가능하니 말씀해 주세요!

6. RAG사용을 위한 함수 생성

LLM모델은 위의 테스트에서 사용한 exaone3.0:8b 이고, Oracle DB안에 로드한 Embbeding Model인 distiluse_base_multilingual_cased_v2을 사용하여 임베딩했습니다.

펑션의 내용을 보면 p_user_question 이라는 변수를 사용자에게 입력 받아옵니다.
입력받은 데이터를 v_model_params에 JSON 타입으로 작성된 모델환경으로 질의를 날립니다.
사용자 질의 내용은 오라클 안의 임베딩 모델을 통해 사용자 질의 쿼리 벡터를 생성하고, 그 쿼리 벡터를 사용하여 DRE.RAG_TEST라는 테이블에 VECTOR_DISTANCE 함수로 벡터거리를 계산합니다.
v_k_stop_count 파라미터의 값만큼 찾고 조회를 STOP합니다. 나온 결과들을 v_sys_instruction에 정의된 내용과 v_message,v_user_question 등을 합하여 v_prompt로 만들어 dbms_vector_chain.utl_to_generate_text를 통해 LLM에 질의를 합니다.

CREATE OR REPLACE FUNCTION DRE.fn_rag_test(p_user_question VARCHAR2) RETURN CLOB  
AUTHID DEFINER
IS
  v_model_params JSON ;
  v_user_question_vec vector; 
  v_prompt varchar2(1000);  
  v_sys_instruction varchar2(1000);
  v_message clob; 
  v_user_question varchar2(1000); 
  v_k_stop_count number := 1;
  output clob;
  
BEGIN
  v_model_params := JSON('
    {
    "provider":"OpenAI",
    "credential_name":"EXAONE_CRED",
    "url": "http://172.17.12.116:9301/v1/chat/completions",
    "model": "exaone3.0:8b",
    "context_length" : 2048
    }') ;
  -- JSON형식에서 질의내용만 추출 :
  v_sys_instruction := 'Please answer with only facts based on the searched content.답변은 한국어로 번역해서 대답해줘';
  v_user_question   := p_user_question ;

  -- 질의내용에 대한 쿼리 벡터 생성
    SELECT TO_VECTOR(vector_embedding(onn.distiluse_base_multilingual_cased_v2 USING v_user_question as data)) as embedding into  v_user_question_vec ;  

           
  -- 텍스트 유사도 검색 (Multi-Vector Similarity Search)

select json_arrayagg(
         json_object('EMBED_ID' is EMBED_ID, 'EMBED_DATA' is EMBED_DATA) 
         returning CLOB) into v_message
from (
  SELECT EMBED_ID ,
       EMBED_DATA
  FROM DRE.rag_test
 ORDER BY VECTOR_DISTANCE(EMBED_VECTOR , v_user_question_vec, COSINE) 
 FETCH FIRST v_k_stop_count ROWS ONLY WITH TARGET ACCURACY 90
 );



  -- 프롬프트생성
  v_prompt := ' 
<s>[INST] {system_instruction}.

Search Data:
{insert_search_data_here}

User Query:
{user_query}

Provide a detailed response based on the search data above. [/INST]
  ';

  v_prompt := replace(replace(replace(v_prompt,'system_instruction',v_sys_instruction),'{insert_search_data_here}', v_message),'{user_query}',v_user_question);

  -- Return the substring of the CLOB within the size limit
  --  output := DBMS_LOB.SUBSTR(v_prompt, 4000, 1);
  utl_http.set_body_charset('UTF-8'); 
output := dbms_vector_chain.utl_to_generate_text(v_prompt, v_model_params);
  RETURN output;
END;
/

7. RAG 실행

위에서 만들 RAG 함수를 사용하여 Ollama 서버에 증강검색을 합니다. 

DECLARE
  p_user_question  CLOB := '마약류관리에관한법률위반(향정) 를 파기환송한 이유에 대해 알려줘';  -- 여기에 p_user_question의 값을 직접 입력
  output CLOB;
BEGIN
  output := DRE.fn_rag_test(p_user_question );
  DBMS_OUTPUT.PUT_LINE('Output: ' || output);
END;
/

-------------------------[Start Time: 2024/09/12 07:46:11]-------------------------
SQL> Output: 마약류관리에 관한 법률 위반(향정) 사건을 파기환송한 이유는 피고인 및 그와 공범관계에 있던 A의 사례로 볼 수 있습니다. 주된 쟁점은 검사 또는 사법경찰관 작성 피의자신문조서의 증거능력이었습니다.

아래는 이를 근거로 한 상세 설명입니다:

1. **검사 또는 사법경찰관 작성 피의자신문조서**: 피고인과 공범인 A에 대한 경우, 이들 작성한 신문조서가 법적으로 증거 능력을 가지는지 여부가 중요한 쟁점으로 다뤄졌습니다.
   
2. ***형사소송법 제312조***: 형사소송법 제312조는 검사 또는 경찰 작성의 피의자신문조서에 대한 규정을 담고 있으며, 이를 통하여 피고인이 진술거부권과 변호인 조력을 받을 권리를 보호하면서도 실질적인 진술 내용이 신뢰할 만한지 평가합니다.
   - 동 조항에 따르면 피의자나 피고인이 경찰이나 검찰 조사 과정에서 자백하거나 진술한 내용이 진정한 것인지를 판단하기 위해 몇 가지 요건들(예: 피고인의 자발성, 임의성)을 충족해야 합니다.

3. **원심 판결**: 원심(아래 단계 법원)은 이러한 형사 소송법 규정과 그 해석에 따라 본 사건에서 검사 또는 사법경찰관 작성 피의자신문조서를 적법하게 인정하고 유죄판결을 내렸습니다. 그러나 위에서 언급된 요건들이 충분히 충족되지 않았다고 판단하여 사후 증거능력이 문제가 되었고 이에 대한 상고가 제기됐습니다.
   
4. **대법원 판결**: 대법원은 원심의 판단이 부족함을 지적하며 사건을 상급심으로 돌려보냈습니다(즉, 파기환송). 대법원은 보다 면밀한 검토를 통해 실제 조사 과정에서 진술 강요 여부와 자발성 등에 대해 엄격히 재검토할 필요성이 있다고 보았던 것입니다.
   - 또한, 구체적인 사실관계 분석 및 관련 법령 적용에 있어서 추가 조사가 요구된 상황이었기 때문으로 추정됩니다.
 
따라서, 마약류관리에 관한 법률위반(향정)을 기소한 본 사건에서는 법원들 간 해석 차이와 이에 따른 심리 부족 등의 문제로 인해 최종 판단은 상급심인 대법원의 재검토 아래 다시 진행되게 된 것입니다.

마치며

테스트를 하면서  신기하다는 느낌은 받았지만, RAG를 활용하여 제품을 만들어서 활용하는 모습은 시간이 조금 걸릴것 같다라는 생각을 했습니다. 하지만, AI기술의 발전 속도를 보면 머지않아 우리 실생활에 빠질 수 없는 중요한 요소가 될 것이라고 생각이 듭니다.

ORACLE DB에서 AI를 활용하여 무엇을 할 수 있다는게 신기했습니다. 제가 테스트한 ORACLE 23AI FREE버전은 23.5인데 dbms_vector_chain.utl_to_generate_text 라는 함수를 사용하여 LLM쪽으로 질의를 하였습니다. 문제는 dbms_vector_chain.utl_to_generate_text 이 함수가 처음에는 VARCHAR2(4000)의 제한이 있었는데 현재 벡터서치 가이드에서는 CLOB로 변경된 것으로 보입니다. 
가이드에서처럼 Ollama Provider제공과 위 함수의 clob 지원이 되는 새로운 버전이 빨리 나왔으면 하는 바램입니다.

들어가며

앞에 글들을 따라 오셨다면 ORACLE23 ai설치와 OML4Py 설치를 끝내셨을겁니다.
사전 학습된 오픈 소스 임베딩 모델이나 자체 임베딩 모델을 사용하여 Oracle Database 외부에서 벡터 임베딩을 생성할 수 있지만, Open Neural Network Exchange(ONNX) 표준과 호환되는 경우 해당 모델을 Oracle Database로 직접 가져올 수도 있습니다.
오라클에서 제공하는 머신러닝용 패키지인 OML4Py를 사용하여 ONNX 형식에 Embedding Model을 ORACLE DB에 로딩하는 방법을 알아보겠습니다.

Model Load

1.     모델을 관리할 스키마 생성

필요에 따라 모델을 관리할 스키마를 생성합니다. 저는 데이터 영역과 모델영역에 서비스 구분을 위해 ONN이라는 스키마를 생성하여 진행하겠습니다.

cd $ORACLE_HOME/oml4py/server
sqlplus / as sysdba
alter session set container=freepdb1;
CREATE TABLESPACE TS_ONN DATAFILE '/u01/oracle/FREE/FREEPDB1/ts_onn_1.dbf' SIZE 100M AUTOEXTEND ON NEXT 100M MAXSIZE 30G EXTENT MANAGEMENT LOCAL AUTOALLOCATE;
@pyquser.sql ONN TS_ONN TEMP unlimited pyqadmin

참고: 23ai부터 create tablespace 시 bigfile이 default값입니다.
Starting with Oracle Database 23ai, BIGFILE functionality is the default for SYSAUX, SYSTEM, and USER tablespaces.

2.     DB에 Directory object 생성

OS에 있는 Model을 DB안으로 가져오기 위해 Directory Object를 생성합니다.

sqlplus / as sysdba
alter session set container=freepdb1;
SQL> alter session set container=freepdb1;
grant read,write on directory MODEL_DIR to ONN;

3.     사전구성된 Model 확인

오라클에서 테스트한 모델을 확인 할 수 있습니다. Free버전이므로 아래에 모델 중 한국어 지원이 되는 'sentence-transformers/distiluse-base-multilingual-cased-v2' 모델을 사용하였습니다.

#명령어
python3
>>> from oml.utils import EmbeddingModel
EmbeddingModelConfig.show_preconfigured()

#결과
'sentence-transformers/all-mpnet-base-v2'
'sentence-transformers/all-MiniLM-L6-v2'
'sentence-transformers/multi-qa-MiniLM-L6-cos-v1'
'ProsusAI/finbert'
'medicalai/ClinicalBERT'
'sentence-transformers/distiluse-base-multilingual-cased-v2'
'sentence-transformers/all-MiniLM-L12-v2'
'BAAI/bge-small-en-v1.5'
'BAAI/bge-base-en-v1.5'
'taylorAI/bge-micro-v2'
'intfloat/e5-small-v2', 'intfloat/e5-base-v2'
'prajjwal1/bert-tiny'
'thenlper/gte-base'
'thenlper/gte-small'
'TaylorAI/gte-tiny'
'infgrad/stella-base-en-v2'
'sentence-transformers/paraphrase-multilingual-mpnet-base-v2'
'intfloat/multilingual-e5-base'
'intfloat/multilingual-e5-small'
'sentence-transformers/stsb-xlm-r-multilingual'

4.     ONNX형식 Embedding Model 다운로드

폐쇄망의 경우 파일을 직접 받아서 서버에 업로드 해야합니다. 업로드 위치는 생성한 디렉토리로 해주세요.

#명령어
python3
>>> from oml.utils import EmbeddingModel
>>> em = EmbeddingModel(model_name="sentence-transformers/distiluse-base-multilingual-cased-v2")
>>> em.export2file("distiluse-base-multilingual-cased-v2",output_dir="./")
/opt/oracle/product/23ai/dbhomeFree/python/lib/python3.12/site-packages/transformers/models/distilbert/modeling_distilbert.py:215: TracerWarning: torch.tensor results are registered as constants in the trace. You can safely ignore this warning if you use this function to create tensors out of constant variables that would be the same every time you call this function. In any other case, this might cause the trace to be incorrect.
  mask, torch.tensor(torch.finfo(scores.dtype).min)

5.     Embedding Model Load

임베딩 모델을 DB에 로드 합니다.

#명령어
sqlplus / as sysdba
alter session set container=freepdb1;

#모델디렉토리:MODEL_DIR
#모델파일:distiluse-base-multilingual-cased-v2.onnx
#스키마.모델명(원하는대로 입력가능):ONN.distiluse_base_multilingual_cased_v2
begin
  DBMS_VECTOR.LOAD_ONNX_MODEL('MODEL_DIR','distiluse-base-multilingual-cased-v2.onnx','ONN.distiluse_base_multilingual_cased_v2',
  JSON('{"function" : "embedding", "embeddingOutput" : "embedding", "input":{"input": ["DATA"]}}'));
end;

6.      Model Load 확인

select * from DBA_MINING_MODELS;

OWNER MODEL_NAME                           MINING_FUNCTION ALGORITHM ALGORITHM_TYPE CREATION_DATE       BUILD_DURATION  MODEL_SIZE   PARTITIONED
----- ------------------------------------ --------------- --------- -------------- ------------------- --------------- ------------ -----------
ONN   DISTILUSE_BASE_MULTILINGUAL_CASED_V2 EMBEDDING       ONNX      NATIVE         2024/08/09 17:17:47    0            540045499    NO

들어가며

오라클의 23ai Document 를 보고 정리한 내용입니다.
ORACLE Document URL :https://docs.oracle.com/en/database/oracle/oracle-database/23/vecse/index.html
23ai 공개 이후 AI에 대해 관심이 생겨 여러 자료들을 찾아보며 RAG(증강검색생성)까지 진행을 해봤습니다.
RAG를 할수록 원본 데이터의 품질이 중요하다고 느껴졌습니다. 
아직 청킹을 잘 하는 방법에 대해서는 이것저것 테스트를 해보고 있습니다.
우선 LLM과 RAG를 하기 전 데이터를 청킹하고 모델을 통해 임베딩을 하는 과정을 소개하려고 합니다.

Embedding이란?

Oracle AI Vector Search는 Oracle Database 내부 또는 외부의 비정형 데이터에서 벡터 임베딩을 자동으로 생성하는 Vector Utilities(SQL 및 PL/SQL 도구)를 제공합니다.
벡터 임베딩 모델은 단어, 문장 또는 단락과 같은 데이터의 각 요소에 숫자 값을 할당하여 임베딩을 만듭니다.
데이터베이스 내에서 임베딩을 생성하려면 ONNX 형식의 벡터 임베딩 모델을 가져와 사용할 수 있습니다. 데이터베이스 외부에서 임베딩을 생성하려면 타사 REST API를 호출하여 타사 벡터 임베딩 모델에 액세스할 수 있습니다.

데이터 변환 단계 이해

입력 데이터는 벡터로 변환되기 전에 여러 단계를 거칠 수 있습니다.

예를 들어, 텍스트 데이터(예: PDF 문서)를 일반 텍스트로 변환한 다음, 결과 텍스트를 더 작은 텍스트 조각(청크)으로 나누어 마지막으로 각 청크에 벡터 임베딩을 생성할 수 있습니다.

위 그림은 입력 데이터가 벡터로 변환되기 전에 통과하는 단계의 파이프라인을 보여줍니다.
1) PDF등의 텍스트를 Chunker가 청크(Chunks)로 생성하고,
2) 생성된 청크를 Tokenizer가 토큰(Tokens)으로 생성하고,
( 별도로 Vocabulary는 토큰이 처리되기 전에 Tokenizer로 전달됩니다.)
3) 토큰이 Embedding Model을 통해 벡터(Vector)로 생성됩니다.
4) 마지막으로 Vector가 Vector Index에 저장되는 것을 보여줍니다.

위의 데이터 변환 파이프라인을 데이터적인 관점에서 조금 더 알아보겠습니다.

각 파이프라인 또는 변환 체인(transformation chain)은 단일 함수 또는 함수 조합을 포함할 수 있으며, 이는 소스 문서가 다른 표현(텍스트, 청크, 요약 또는 벡터)으로 변환될 때 적용됩니다.
각 체인 가능 유틸리티 함수는 데이터를 다른 표현으로 변환하는 특정 작업을 수행합니다. 예를 들어 데이터를 텍스트로 변환하거나, 텍스트를 청크로 변환하거나, 추출된 청크를 임베딩으로 변환하는 작업을 수행합니다. 

체인 가능한 유틸리티 함수는 유연하고 모듈화되도록 설계되었습니다.
위 그림에서 볼 수 있듯이 파일-텍스트-청크-임베딩 체인은 다음 순서로 일련의 작업을 수행합니다.

①     PDF 파일을 일반 텍스트로 변환합니다(UTL_TO_TEXT)
②     결과 텍스트를 적절한 크기의 청크로 분할합니다(UTL_TO_CHUNKS)
③     각 청크에 벡터 임베딩을 생성합니다(UTL_TO_EMBEDDINGS)

파일-텍스트-청크-임베딩 체인을 쿼리를 통해 확인해보겠습니다.

파일을 일반 텍스트로 변환(UTL_TO_TEXT)

select 
dbms_vector_chain.utl_to_text(TO_BLOB(bfilename('DOC_DIR',a.file_name))) AS DOC_content_blob
from (values('대한민국 헌법.pdf')) a (file_name) ;

텍스트로 변환된 데이터를 청킹(UTL_TO_CHUNKS)

select t.*
  FROM (select 
dbms_vector_chain.utl_to_text(TO_BLOB(bfilename('DOC_DIR',a.file_name))) AS DOC_content_blob
from (values('대한민국 헌법.pdf')) a (file_name) ) dc 
CROSS JOIN TABLE (
                 dbms_vector_chain.utl_to_chunks(
                 dbms_vector_chain.utl_to_text(dc.DOC_CONTENT_BLOB)
       ,json('{"by":"characters","max":"3000","split":"none","normalize":"all","LANGUAGE":"KOREAN"}'))) t;

parameter :

• BY:CHARACTERS(문자 수를 세어 나눔)
• MAX:3000(각 청크의 최대 크기에 대한 제한을 지정합니다. 최대 크기 제한에 도달하면 데이터를 분할합니다.)
• SPLIT:NONE(입력 텍스트가 최대 크기 제한에 도달했을 때 분할할 위치를 지정합니다. NONE은 한계 에서 분할하는 의미)
• NORMALIZE:all(문서를 텍스트로 변환할 때 발생할 수 있는 문제(여러 개의 연속된 공백 및 smart quotes(굽은 따옴표(‘’,“”)) 등)를 자동으로 전처리하거나 후처리합니다. all=유니코드 구두점을 standard single-byte로 정규화합니다.)
• LANGUAGE:KOREAN(언어는 한국어)

각 청크에 벡터 임베딩을 생성(UTL_TO_EMBEDDINGS)

select t.*
  FROM (select 
dbms_vector_chain.utl_to_text(TO_BLOB(bfilename('DOC_DIR',a.file_name))) AS DOC_content_blob
from (values('대한민국 헌법.pdf')) a (file_name) ) dc 
CROSS JOIN TABLE (
                 dbms_vector_chain.utl_to_embeddings(
                 dbms_vector_chain.utl_to_chunks(
                 dbms_vector_chain.utl_to_text(dc.DOC_CONTENT_BLOB)
                    ,json('{"by":"characters","max":"3000","split":"none","normalize":"all","LANGUAGE":"KOREAN"}')),
                        json('{"provider":"database", "model":"ONN.DISTILUSE_BASE_MULTILINGUAL_CASED_V2"}'))) t
CROSS JOIN JSON_TABLE(t.column_value, '$[*]' COLUMNS ( embed_vector CLOB PATH '$.embed_vector')) AS et;

 [표: 제공되는 체인 가능한 유틸리티 함수]

기능	설명	입력 및 반환 값
UTL_TO_TEXT()	데이터(예: Word, HTML 또는 PDF 문서)를 일반 텍스트로 변환합니다.	CLOB 또는 BLOB로 입력을 허용합니다. 문서의 일반 텍스트 버전을 CLOB로 반환합니다
UTL_TO_CHUNKS()	데이터를 청크로 변환합니다.	입력을 일반 텍스트(CLOB 또는VARCHAR2)로 허용합니다. 데이터를 분할하여 청크 배열(CLOB)을 반환합니다.
UTL_TO_EMBEDDING()	데이터를 단일 임베딩으로 변환합니다.	입력을 일반 텍스트(CLOB)로 허용합니다. 단일 임베딩(VECTOR)을 반환합니다.
UTL_TO_EMBEDDINGS()	청크 배열을 임베딩 배열로 변환합니다.	입력을 청크 배열(VECTOR_ARRAY_T)로 허용합니다. 임베딩 배열(VECTOR_ARRAY_T)을 반환합니다.
UTL_TO_SUMMARY()	크거나 복잡한 문서와 같은 데이터에 대한 간결한 요약을 생성합니다.	입력을 일반 텍스트(CLOB)로 허용합니다. 일반 텍스트의 요약을 CLOB로 반환합니다.
UTL_TO_GENERATE_TEXT()	프롬프트에 대한 텍스트를 생성합니다.	입력을 텍스트 데이터(CLOB)로 허용합니다. 이 정보를 처리하여 생성된 텍스트가 포함된 CLOB를 반환합니다.

 

청크(Chunk) 작업

임베딩에서 알고리즘도 중요하지만 가장 중요한 것중 하나는 긴 문서를 어떻게 파편으로 잘라낼것인가? (이를 영어로 Chunking이라고 한다.) 입니다.
오라클 데이터베이스는 텍스트를 분할을 위한 유틸리티 패키지인 DBMS_VECTOR_CHAIN 패키지를 제공합니다. 문서용 텍스트 데이터, 텍스트 데이터의 청크 분할, 콘텐츠 요약 및 임베딩을 모두 데이터베이스내에서 처리할수 있습니다.
청킹 기능은 VECTOR_CHAIN 패키지 내 VECTOR_CHUNKS 함수를 통해  사용이 가능합니다.
데이터를 일반 텍스트로 변환한 다음 결과 텍스트를 Chunker로 전달합니다. 그런 다음 chunker는 chunking 이라는 프로세스를 사용하여 텍스트를 더 작은 청크로 나눕니다.
청킹에는 세부적인 파라미터들이 많아 아래에 표에 정리하였습니다.

VECTOR_CHUNKS parameters

Parameter	Description and Acceptable Values
BY	데이터 분할 모드를 지정합니다. 즉, 문자, 단어 또는 어휘 토큰의 수를 세어 분할합니다. 유효한 값 : ·       BY CHARACTERS(또는 BY CHARS): 문자 수를 세어 나눕니다. ·       BY WORDS: 단어의 개수를 세어 나눕니다. 단어는 알파벳 문자 시퀀스, 숫자 시퀀스, 개별 구두점 또는 기호로 정의됩니다. 공백 단어 경계가 없는 분할 언어(예: 중국어, 일본어 또는 태국어)의 경우 각 모국어 문자는 단어(즉, 유니그램)로 간주됩니다. ·       BY VOCABULARY: 어휘 토큰의 개수를 세어 나눕니다. 어휘 토큰은 임베딩 모델이 사용하는 토크나이저의 어휘로 인식되는 단어 또는 단어 조각입니다. VECTOR_CHUNKS  helper API 사용하여 어휘 파일을 로드할 수 있습니다 DBMS_VECTOR_CHAIN.CREATE_VOCABULARY. 참고 : 정확한 결과를 얻으려면 선택한 모델이 청크에 사용된 어휘 파일과 일치하는지 확인하십시오. 어휘 파일을 사용하지 않는 경우 입력 길이가 모델의 토큰 제한 내에서 정의되었는지 확인하십시오. 기본값 :BY WORDS
MAX	각 청크의 최대 크기에 대한 제한을 지정합니다. 이 설정은 더 큰 텍스트에서 최대 제한이 발생하는 고정된 지점에서 입력 텍스트를 분할합니다. 단위는 모드 MAX에 해당합니다 BY. 즉, 특정 수의 문자, 단어, 숫자, 구두점 또는 어휘 토큰의 최대 크기 제한에 도달하면 데이터를 분할합니다. 유효한 값 : ·       BY CHARACTERS: 50 to 4000 characters ·       BY WORDS: 10 to 1000 words ·       BY VOCABULARY: 10 to 1000 tokens 기본값 :MAX 100
SPLIT [BY]	입력 텍스트가 최대 크기 제한에 도달했을 때 분할할 위치를 지정합니다. 이는 청크에 대한 적절한 경계를 정의하여 관련 데이터를 함께 유지하는 데 도움이 됩니다. Valid values: 1.    NONE: MAX문자, 단어 또는 어휘 토큰의 한계 에서 분할됩니다 .   2.    NEWLINE, BLANKLINE, and SPACE: MAX 값 이전의 마지막 분할 문자에서 분할되는 단일 분할 문자 조건입니다. NEWLINE을 사용하여 텍스트 행의 끝에서 분할합니다. BLANKLINE을 사용하여 공백 행의 끝(예: 두 줄의 새 행)에서 분할합니다. SPACE를 사용하여 공백 행의 끝에서 분할합니다.   ·       RECURSIVELY: 이것은 문자(또는 시퀀스)의 순서대로 나열된 목록을 사용하여 입력된 텍스트를 깨는 다중 분할 문자 조건입니다. RASCERIESS는 다음 순서로 블랭크 라인, 새 라인, 스페이스, 없음으로 미리 정의됩니다: 1. 입력 텍스트가 MAX 값보다 크면 첫 번째 분할 문자로 분할합니다. 2. 실패할 경우 두 번째 분할 문자로 분할합니다. 3. 등등. 4. 분할 문자가 없는 경우 텍스트에 표시되는 곳마다 MAX로 분할합니다.   ·       SENTENCE: 문장 경계에서 입력된 텍스트를 끊는 문장 끝 분할 조건입니다. 이 조건은 입력 언어의 문장 문장부호에 대한 지식과 문맥 규칙을 사용하여 문장 경계를 자동으로 결정합니다. 이 언어별 조건은 대부분 EOS(End-of-Sentence) 문장부호와 일반적인 약어에 의존합니다. 문맥 규칙은 단어 정보를 기반으로 하므로 이 조건은 텍스트를 단어 또는 어휘로 분할할 때만 유효합니다(not by characters). Note: 이 조건은 BY WORD 및 MAX 설정을 따르므로 경우에 따라 정확한 문장 경계를 결정할 수 없습니다. 예를 들어, 문장이 MAX 값보다 크면 MAX에서 문장을 분할합니다. 마찬가지로 MAX 한계 내에 맞는 경우에만 텍스트에 여러 문장을 포함합니다.   ·       CUSTOM: 사용자 정의 분할 문자 목록에 따라 분할합니다. 각각 최대 10개의 길이로 최대 16개의 분할 문자 문자열로 사용자 정의 시퀀스를 제공할 수 있습니다. 다음과 같이 유효한 텍스트 리터럴을 제공합니다: tab(\t), newline(\n), linefeed (\r)에 대해서만 시퀀스를 생략할 수 있습니다. Default value: RECURSIVELY
OVERLAP	청크가 포함해야 할 이전 텍스트의 양(양의 정수 리터럴 또는 0)을 지정합니다. 이는 이전 청크 텍스트의 일부 양을 포함하여 관련 텍스트(예: 문장)를 논리적으로 분할하는 데 도움이 됩니다. 중복의 양은 청크의 최대 크기를 측정하는 방법(문자, 단어 또는 어휘 토큰)에 따라 달라집니다. 중복은 지정된 SPLITE 조건(예를 들어 NEWLINE에서)에서 시작됩니다. Valid value: 5% to 20% of MAX Default value: 0
LANGUAGE	입력 데이터의 언어를 지정합니다. 이 절은 특히 텍스트에 다른 언어로 다르게 해석될 수 있는 특정 문자(예: 구두점 또는 약어)가 포함되어 있는 경우 중요합니다. Valid value: Oracle Database Globalization Support Guide에 나열된 모든 NLS 지원 언어 이름 또는 언어 약어. 공백이 있는 모든 언어 이름에는 반드시 double quotation(")을 사용해야합니다. For example: LANGUAGE "simplified chinese"   한 단어 언어 이름의(one-word language names) 경우 quotation 표시가 필요하지 않습니다. For example: LANGUAGE american   Note: DBMS_VECTOR_CHAIN.CREATE_LANG_DATA chunker helper API를 사용하여 지정된 언어에 대해 언어별 데이터(약어 tokens)를 데이터베이스에 로드할 수 있습니다. Default value: NLS_LANGUAGE from session
NORMALIZE	문서를 텍스트로 변환할 때 발생할 수 있는 문제(여러 개의 연속된 공백 및 smart quotes(굽은 따옴표(‘’, “”)) 등)를 자동으로 전처리하거나 후처리합니다. 오라클은 이 모드를 사용하여 품질이 좋은 청크를 추출하는 것을 권장합니다. Valid values: ·       NONE: 정규화를 지정하지 않습니다. ·       ALL: 공통 다중 바이트(유니코드) 구두점을 standard single-byte로 정규화합니다. ·       PUNCTUATION: smart quotes, smart hyphens 및 기타 단일 바이트 구두점과 동일한 멀티 바이트를 포함합니다. For example: o   2018u 'map to 0027' o   2019u 'map to 0027' o   201Bu 'map to 0027' ·       WHITESPACE: 불필요한 문자를 제거하여 공백을 최소화합니다. For example, blanklines은 유지하되, 추가로 newlines,spaces,tabs 는 제거합니다: " \n \n " => "\n\n" ·       WIDECHAR: 넓고 다중 바이트인 숫자와 (az) 문자를 단일 바이트로 정규화합니다. 0-9 및 a-z A-Z로 된 다중 바이트이며 , ZH/JA 형식 텍스트로 표시할 수 있습니다. Note: 쉼표로 구분된 여백(WHITESPACE), 구두점(PUNCTUATION), and  WIDECHAR 괄호 목록(WIDECHAR in parentheses)을 반드시 지정해야합니다. Default value: None
EXTENDED	MAX_STRING_SIZE 매개 변수를 EXTED로 설정할 필요 없이 VARCHAR2 문자열의 출력 제한을 32767bytes로 늘립니다. Default value: 4000 or 32767 (when MAX_STRING_SIZE=EXTENDED)

 

들어가며

최근 인공지능 기술의 발전으로 다양한 분야에서 혁신을 일으키고 있습니다. 하지만 ChatGPT 를 사용하면서 느꼈던 점은 일반적인 내용으로만 답변을 하며 전문적이거나 내가 가진 데이터들을 활용하기 힘들다는 점이었습니다.

이러한 한계를 극복하기 위해 Privit한 정보를 활용하여 LLM을 사용할 수 없을까해서 나온것이 벡터 DB를 활용한 RAG입니다.

검색 증강 생성인 RAG에 대해서 DBA적 측면에서 간단하게 설명을 하고 들어가겠습니다.

RAG(검색 증강 생성)란?

검색 증강 생성(Retrieval Augmented Generation, RAG) 는 DB에 있는 정보 등의 별도 정보원을 제공하여 환각 현상을 방지하고 사용자가 원하는 LLM의 답변 품질을 개선한 프로세스입니다.

Oracle AI Vector Search는 벡터를 관계형 데이터, 그래프 데이터, 공간 데이터 및 JSON 컬렉션과 결합할 수 있는 정교한 쿼리를 구현하기 위해 Enterprise Retrieval Augmented Generation(RAG)을 지원합니다.

검색 증강 생성은 LLM의 한계를 해결하기 위해 개발된 접근 방식입니다.

§   RAG는 사전 학습된 언어 모델의 강점과 응답 생성 중에 데이터 세트 또는 데이터베이스에서 최신의 정확한 정보를 실시간으로 검색하는 기능을 결합합니다.

§   RAG 구현을 통해 LLM과 소통하고 AI 벡터 검색을 통해 발견된 비즈니스 데이터로 LLM의 지식이 증가합니다.

GPT(Generative Pretrained Transformer)와 같은 LLM의 주요 문제는 마지막 업데이트 시점까지 훈련받은 패턴과 데이터에만 기반하여 응답을 생성한다는 것입니다.

즉, 훈련이 중단된 후에는 새로운 실시간 정보에 액세스하거나 통합할 수 있는 능력이 본질적으로 부족하여 오래되거나 불완전한 정보에 대한 응답이 제한될 수 있습니다.

LLM은 개인의 환경에 특화된 데이터를 알지 못하고 일반적인 데이터정보만 가지는 한계가 있습니다.

따라서 LLM이 지닌 한계인 일반적인 데이터정보를 극복하기 위해 ORACLE DB내에 정보까지 확장시켜 조회하는 RAG를 구축하게 되었습니다.